NBDT论文将决策树思想应用到神经网络最后的全连接层来分类,做出一个层级的分类模型,这样就能看出一张图片是怎么被分到具体类别的。这里主要说一下决策树是怎么代替全连接层的,其他优化建议阅读原论文。
论文链接:https://arxiv.org/abs/2004.00221
Related work
解决神经网络可解释性通常从两方面,一是可视化图像中的显著性区域,二是可视化决策分类的过程。如下面两张图:
图1. 通过显著性区域解释神经网络

图2. 可视化神经网络决策过程

Contribution
- 提出一个树监督损失,比原始网络效果提高2%。
- 为倾斜的决策树提出一个备选层次结构,包括利用预训练网络建树和利用已有的分层结构(比如WordNet)。就是怎么建树。
- 文章显示了NBDT的可解释性对错分的样本很有帮助,有利于确定模棱两可的样本。
Method
本篇文章着眼于可视化神经网络的决策过程,通过引入决策树,将神经网络分类的过程展现出来。
文章将神经网络最后的全连接层取消,用决策树代替。但是只用了决策树的思想,而没有使用它分类节点的准则(传统准则是特征大于 x 为A类,小于 x 为B类),因为决策树传统分类的准则不方便于参数反向传播调整模型。
图3:
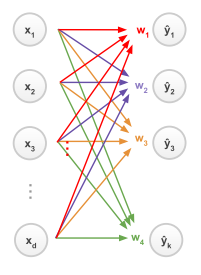
上图是全连接层分类的过程,左侧是神经网络输出的d维的特征向量,右侧表示k个类别,右侧 y 的值越大,属于这个类别的概率就越大。
图3中,y1=x·w1,y2=x·w2 …. 取最大的y,将样本归为此类别。
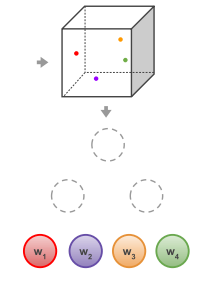
文章中的决策树利用这一过程,将w向量的值作为节点,如图4,特征x与节点上的每个值相乘,大的胜出,样本归为此类。
图4:
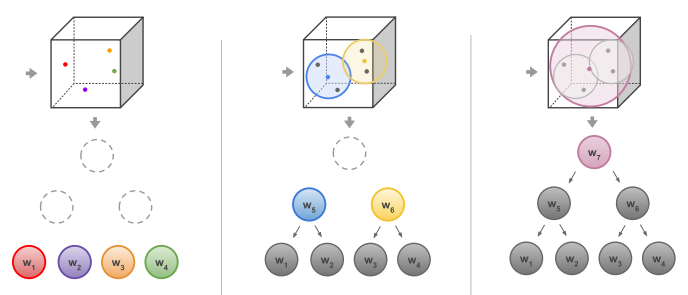
同时可以这样理解,w1和w2如果相似,那么这两个类别就很相似,可以归为一个大类,让后让他们连到同一个父节点上,如图5,父节点 w5 取两个子节点w1和w2的平均值作为他们的大类。这样假设w5 和 w6 是两个大类,划分的时候将特征 x 与w5、w6 相乘取较大的作为划分的大类。
图5:
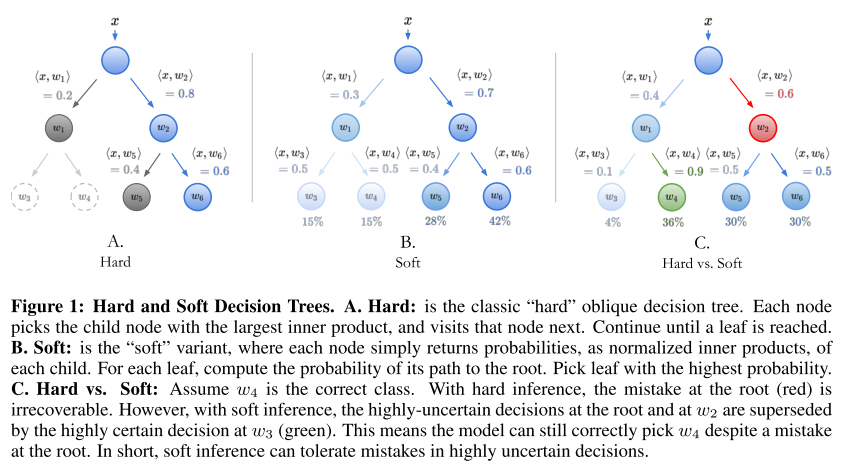
所以本文做决策的过程就如下图6所示,将神经网络输出特征与决策树上所有节点 w 相乘,得到最后的分类结果。当然下图C中是一个会错误决策的过程,文章中也给出了相应的优化方法。
图6:
决策树的分层结构是通过对 k 个类别的 w 层次聚类得出的,但是神经网络刚开始时全连接层权重是没含义的,聚类没法得出好的结构。所以需要先预训练得出比较好的全连接层权重,然后加入决策树结构微调模型。决策树的分层结构也可以根据实际含义自己设定,具体方法文章中写的有。
这个模型的本质还是全连接那种相乘的方法,只不过加入了层次的结构抽象出来一些父类来观察神经网络决策的过程。因此效果能达到和神经网络基本相同的准确率,而其他加入决策树的方法则会降低神经网络的准确率。
它还有一个优点就是如果给了一张类别中没有的图片,根据模型做出的决策图,能够知道它是怎么划分的,大概应属于哪个类别。